计算n的阶乘

• 迭代

  int result = 1;
  for(int i=1; i<=n; i++){
    result = result * i;
  }
  

• 递归

  int factorial(int n){
    if(n == 1){
        return 1;
    }
    return n * factorial(n - 1);
  }
  

  此递归的栈如下：

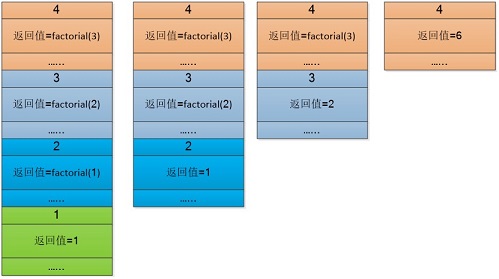
问题 当n过大时，容易出现StackOverflowError，这是因为需要求解的子问题过多，递归嵌套层次过深。在C，Erlang等语言中支持尾递归，可以对这种场景进行优化，但Python，Java等语言在编译器级别并不支持尾递归技术，据说可以借助Lambda表达式来实现，但目前还没具体研究。我们先来看下什么是尾递归。

尾递归

当递归调用是函数体中最后执行的语句并且它的返回值不属于表达式一部分时，这个递归就是尾递归。具体如下:

function factorial(int n) {
   if (n === 1) return 1;
   return n * factorial(n-1); // 最后一步不是调用自身，因此不是尾递归
}

function factorial(int n ,int result) {
   if (n === 1) return result;
   return factorial(n-1, n * result); // 最后一步不是调用自身，因此不是尾递归
}

使用尾递归可以带来一个好处：因为进入最后一步后不再需要参考外层函数（caller）的信息，因此没必要保存外层函数的stack，递归需要用的stack只有目前这层函数的，因此避免了栈溢出风险。一些语言提供了尾递归优化，当识别出使用了尾递归时，会相应地只保留当前层函数的stack，节省内存。所以，在没有尾递归优化的语言，如java, python中，鼓励用迭代iteration来改写尾递归；在有尾递归优化的语言如Erlang中，鼓励用尾递归来改写其他形式的递归。